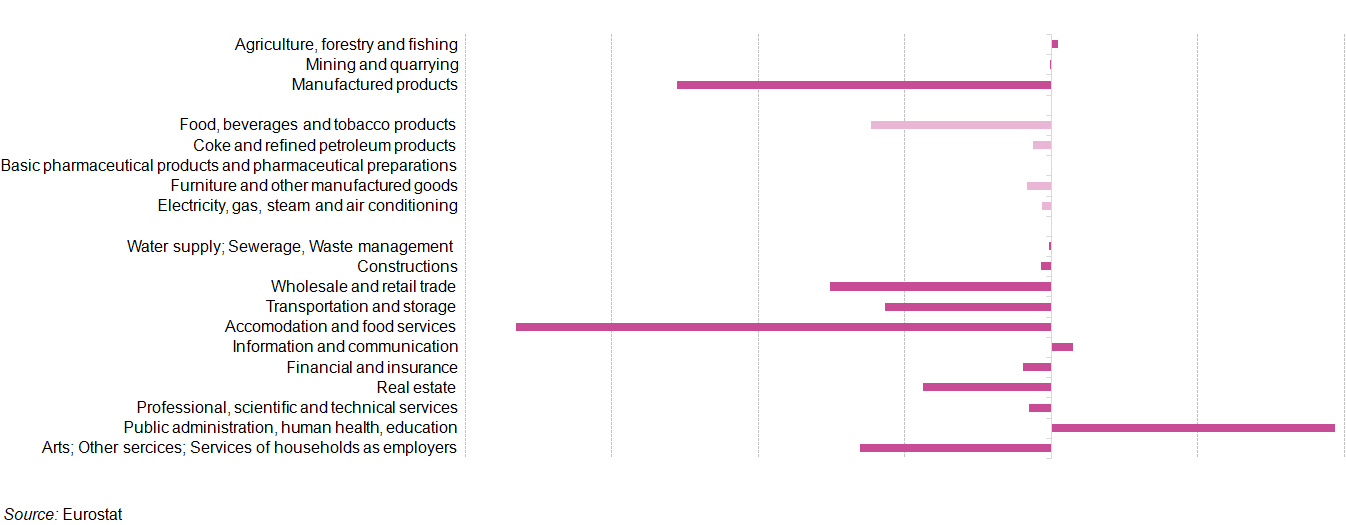
I – DÉFINITIONS
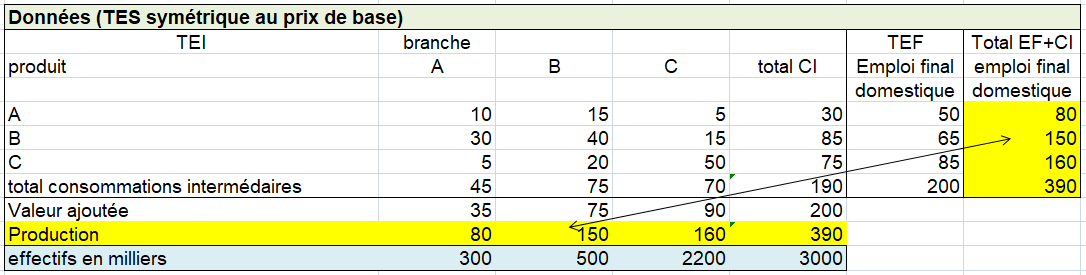
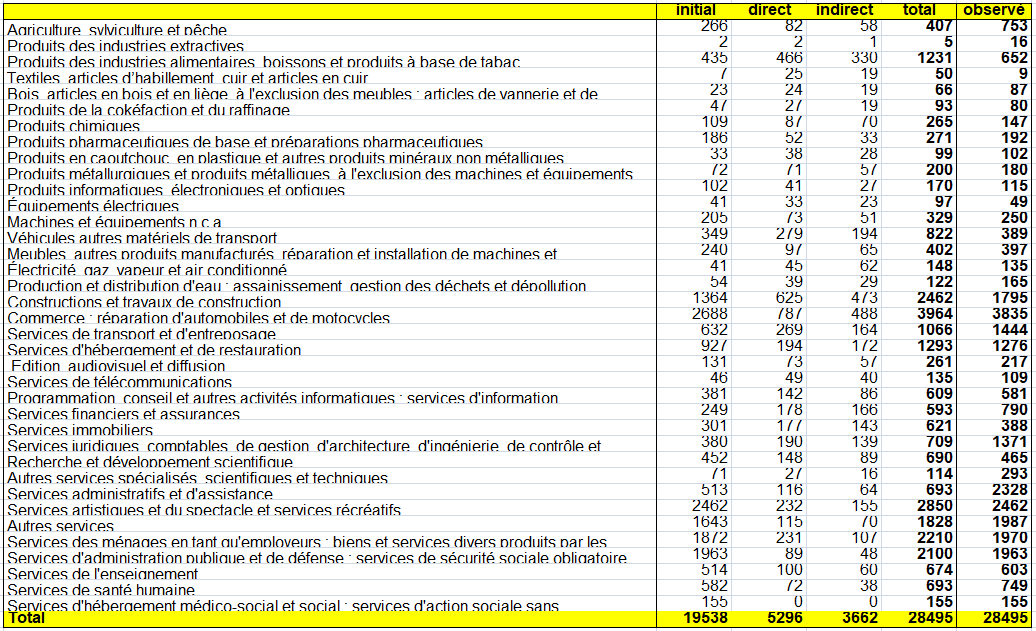
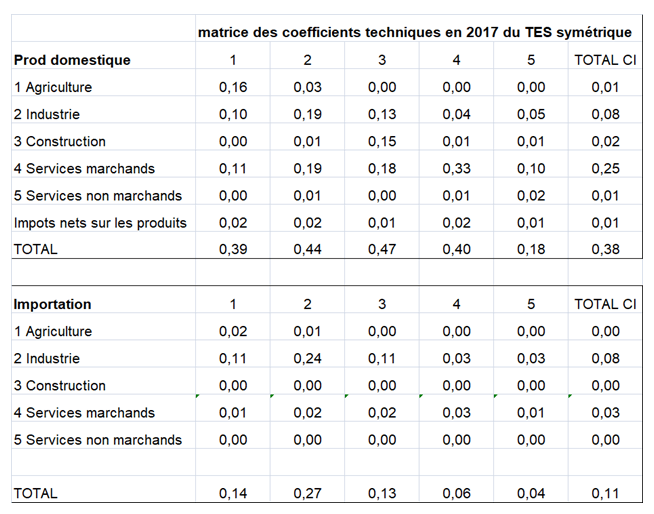
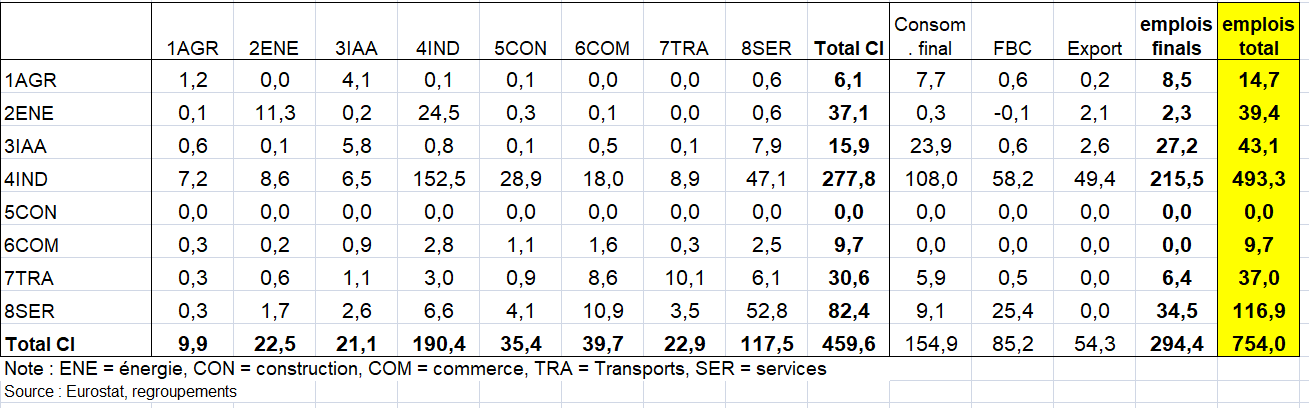
Le TES symétrique intègre en un seul tableau les emplois et les ressources. Les totaux en ligne (total des emplois) sont égaux aux totaux en colonne (total des ressources). Un TES symétrique est généralement de taille plus modeste que le TRE. Le TES symétrique peut être :
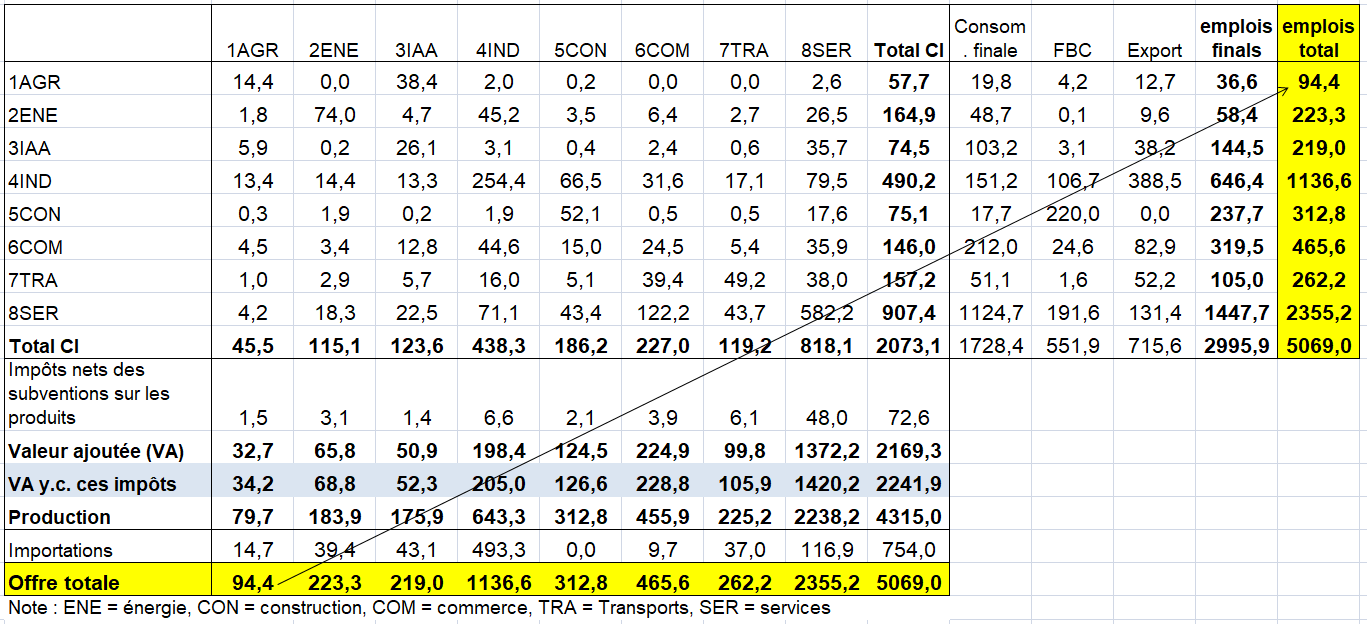
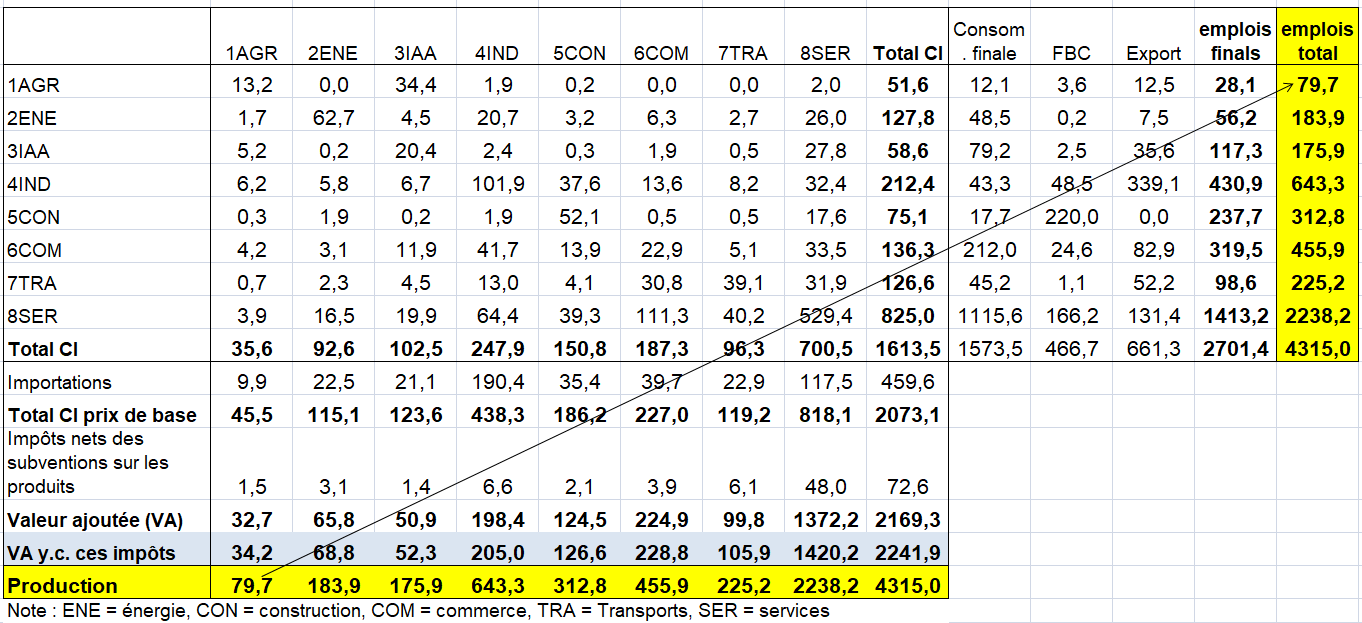
– soit de type « produit * produit » : (quels produits sont utilisés pour la production de tels autres produits par les UPH ?),
– soit de type « branche d’établissement x branche d’établissement » (« industry » en anglais se traduit ici par branche d’établissement et non par industrie au sens industrie manufacturière) : quelles branches d’activité principale (ou quels secteurs d’activité) utilisent la production de quelles autres branches d’activité principale (respectivement secteurs d’activité) ?
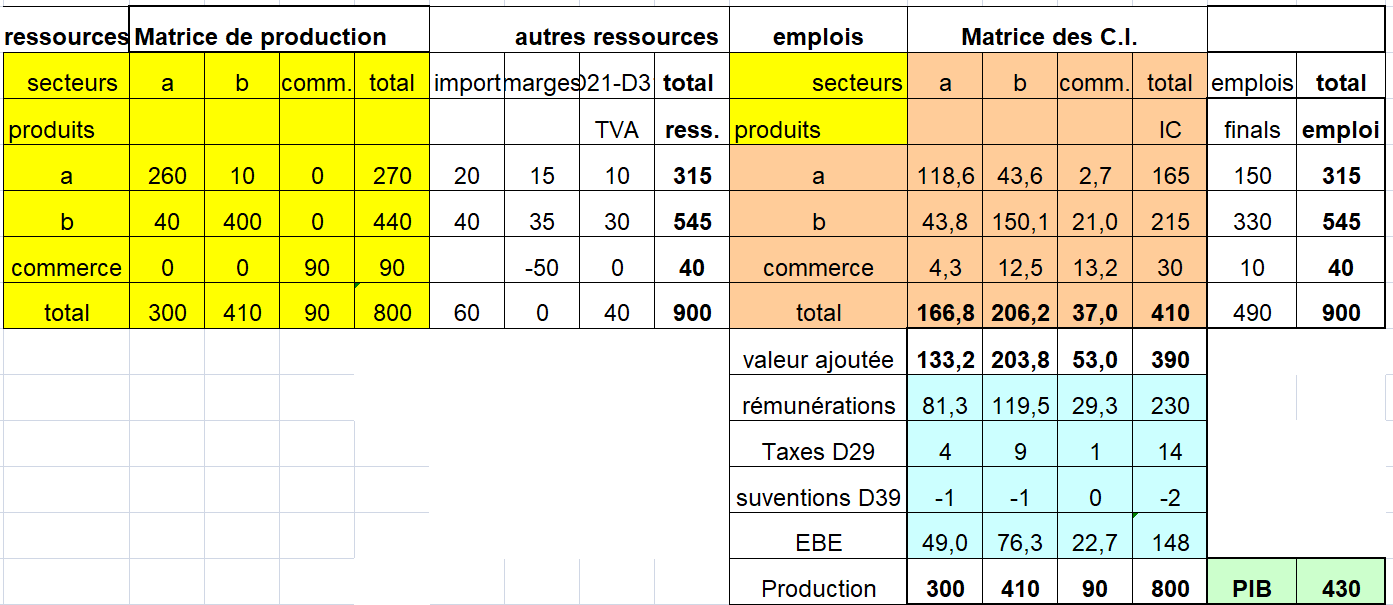
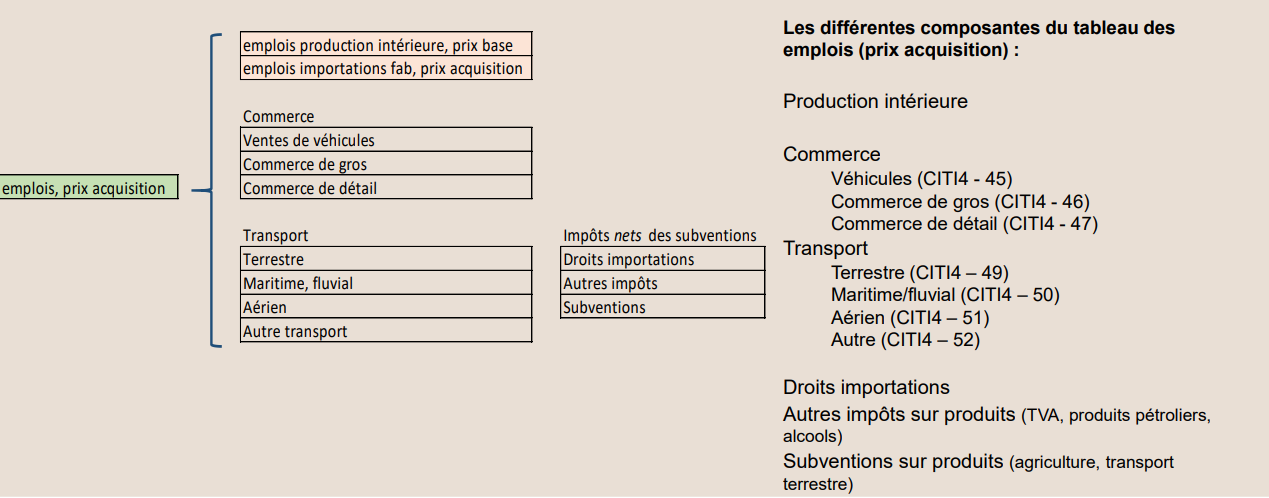
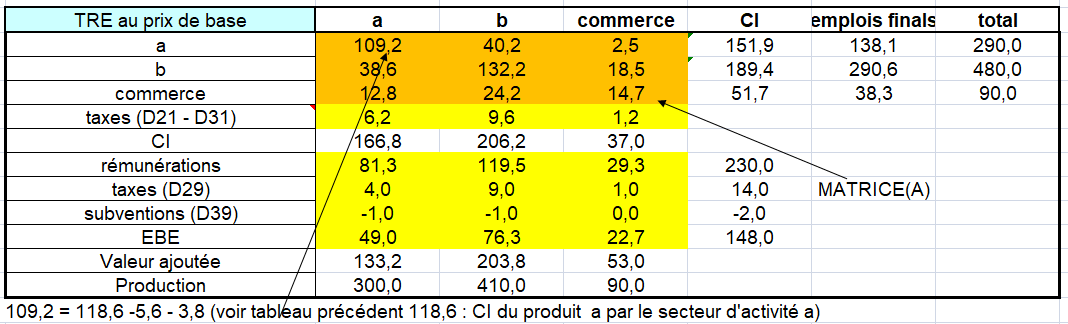
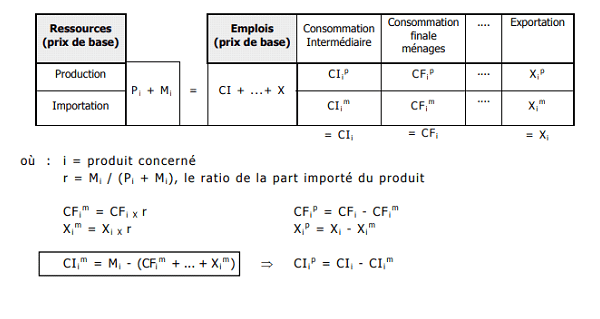
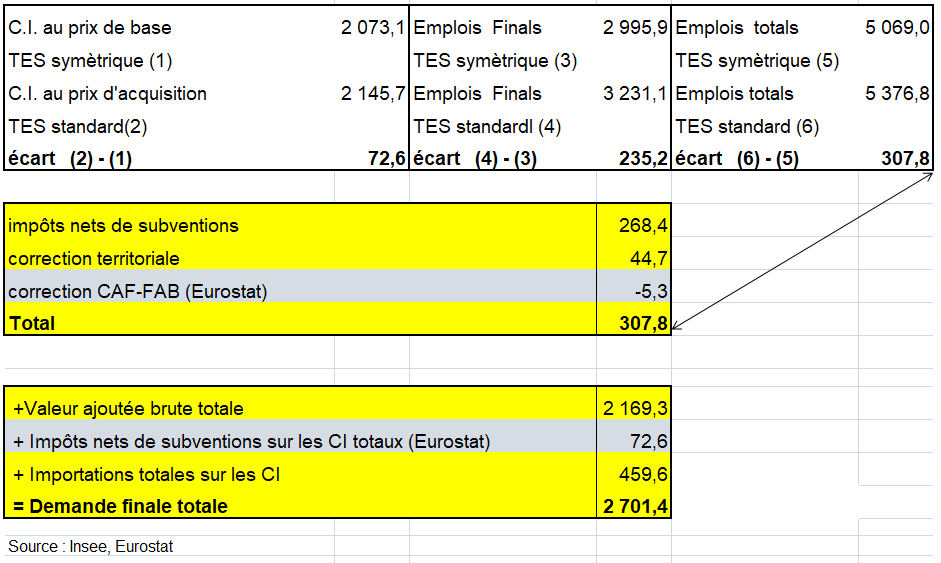
Le SEC 2010 préconise un tableau entrées-sorties produit x produits. II s’ensuit que la structure des entrées intermédiaires et primaires données dans les tableaux des emplois pour les branches hétérogènes doit être transformée en une structure d’entrées pour les produits. Le volet des emplois finals peut quant à lui être tout simplement repris du tableau des emplois valorisés aux prix de base.
Le projet FIGARO d’Eurostat accepte toutefois les TES symétriques par produit et par branche d’établissement.
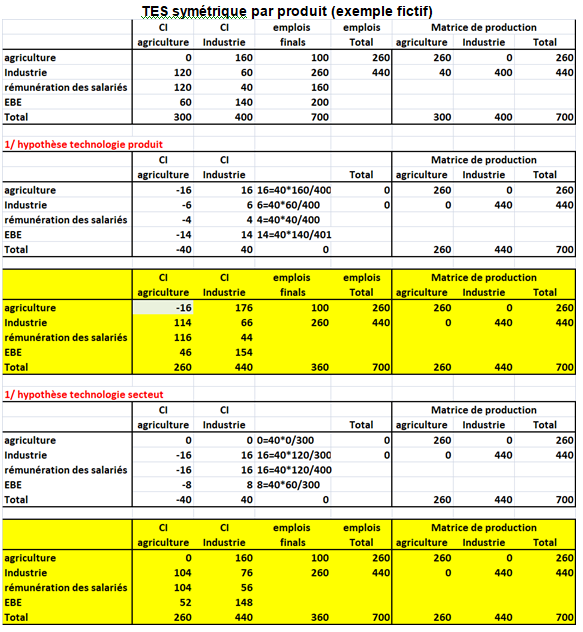
Pour les TES symétriques de type « produit * produit » , les deux hypothèses sont les suivantes :
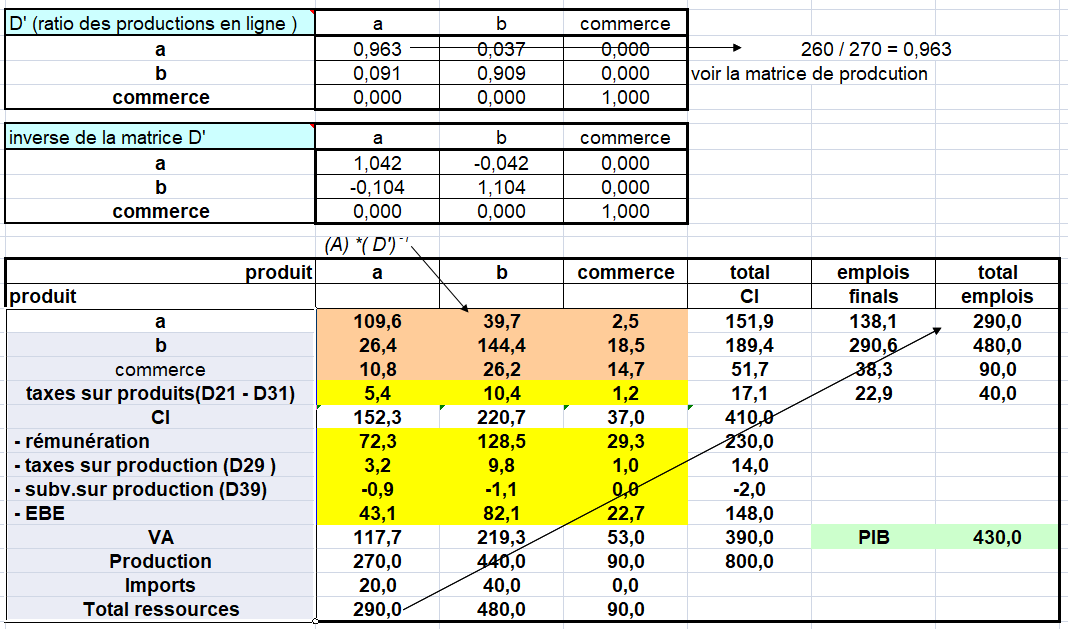
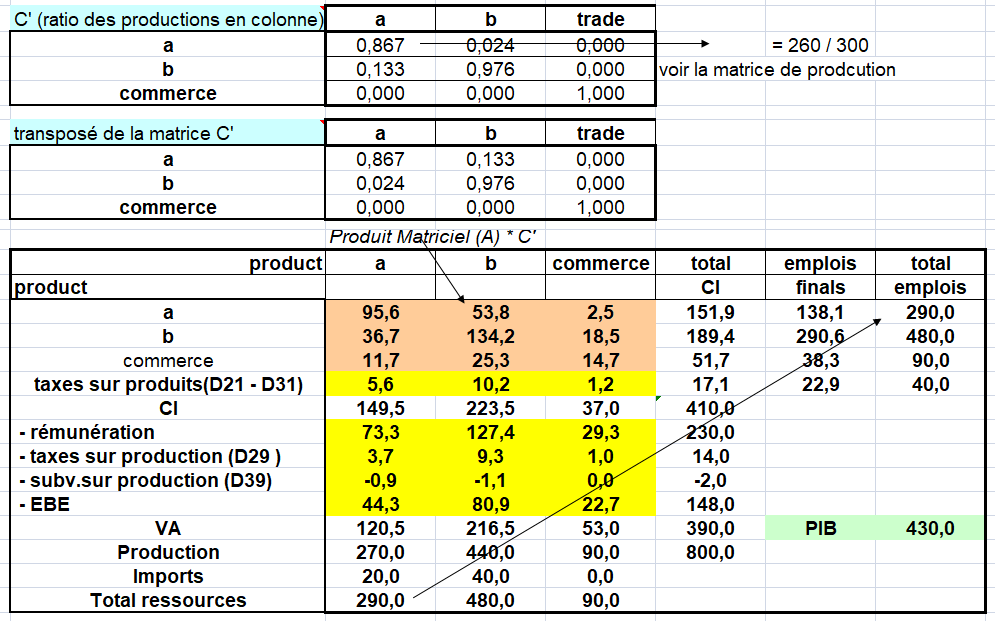
1/ La première hypothèse est la technologie produit : chaque produit a sa propre structure de production quelle que soit le secteur d’établissement ou d’entreprise qui le fabrique.
2/ Dans l’hypothèse technologie secteur, tous les produits fabriqués par un secteur d’établissement ou d’entreprise le sont avec la même combinaison d’entrées.
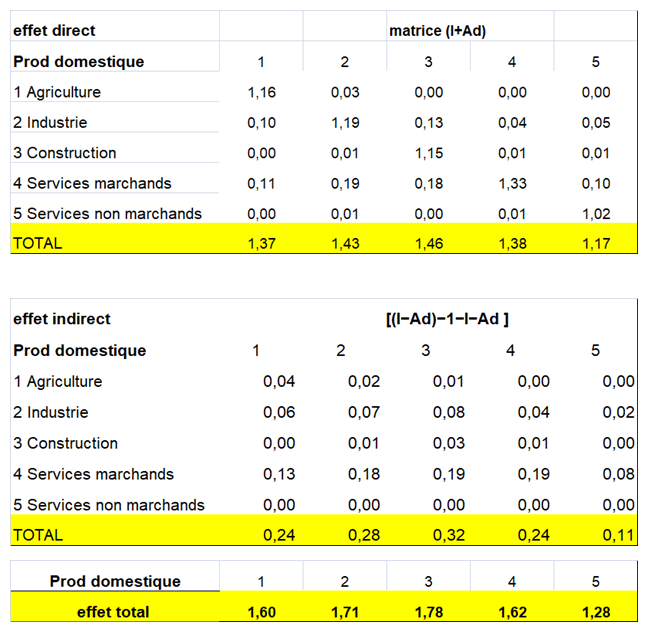
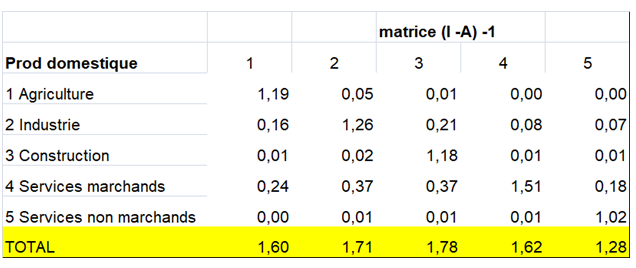
Ces deux modèles ont été développés par Richard Stone et sont repris dans l’ancienne version du SCN, le SNA de 1968. Ce système a officiellement introduit le lien entre les comptes nationaux et les tableaux entrées-sorties via le stade intermédiaire des tableaux des ressources et des emplois. Cette partie du SNA 1968 n’a pas été reprise par le SEC 79 qui englobait des tableaux entrées-sorties mais pas de tableaux emplois-ressources. Ces deux hypothèses ont été combinées dans des modèles de technologies hybrides, et introduites dans le SNA 68. En pratique, pour pouvoir appliquer de tels modèles, des matrices de transformation sont dérivées du tableau des ressources et sont ensuite appliquées aux volets intermédiaire et primaire du tableau des emplois.
Les manuels du SNA 93 et du SEC 1995 privilégient la technologie unique par produit. Le principe d’une technologie unique par secteur d’activité est très peu crédible, voire même absurde dans certains cas. Les secteurs d’activité industriels ont, la plupart du temps, une production secondaire importante d’activités de commerce de gros. L’application dans ce cas du principe d’une technologie unique par secteur d’activité implique l’allocation d’inputs industriels (matières premières, produits semi-finis) aux activités de commerce de gros, ce qui est insensé. De plus, certains ont montré qu’un tableau entrées-sorties basé sur la technologie unique par secteur d’activité ne peut être utilisé comme instrument d’analyse économique. Et c’est précisément la raison d’être des tableaux entrées-sorties.
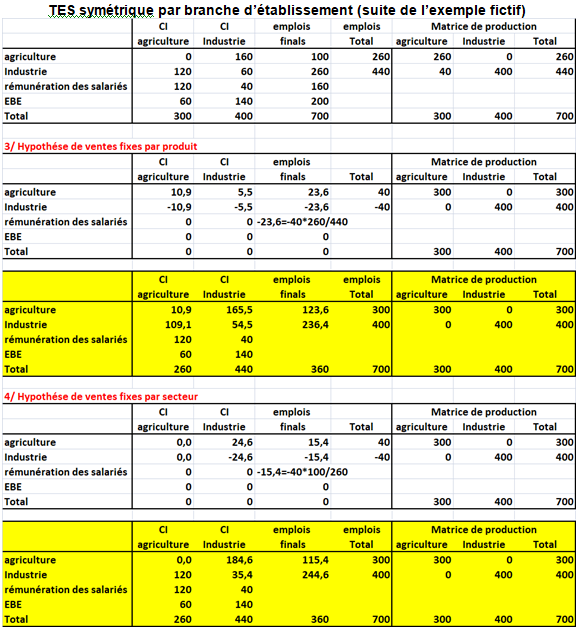
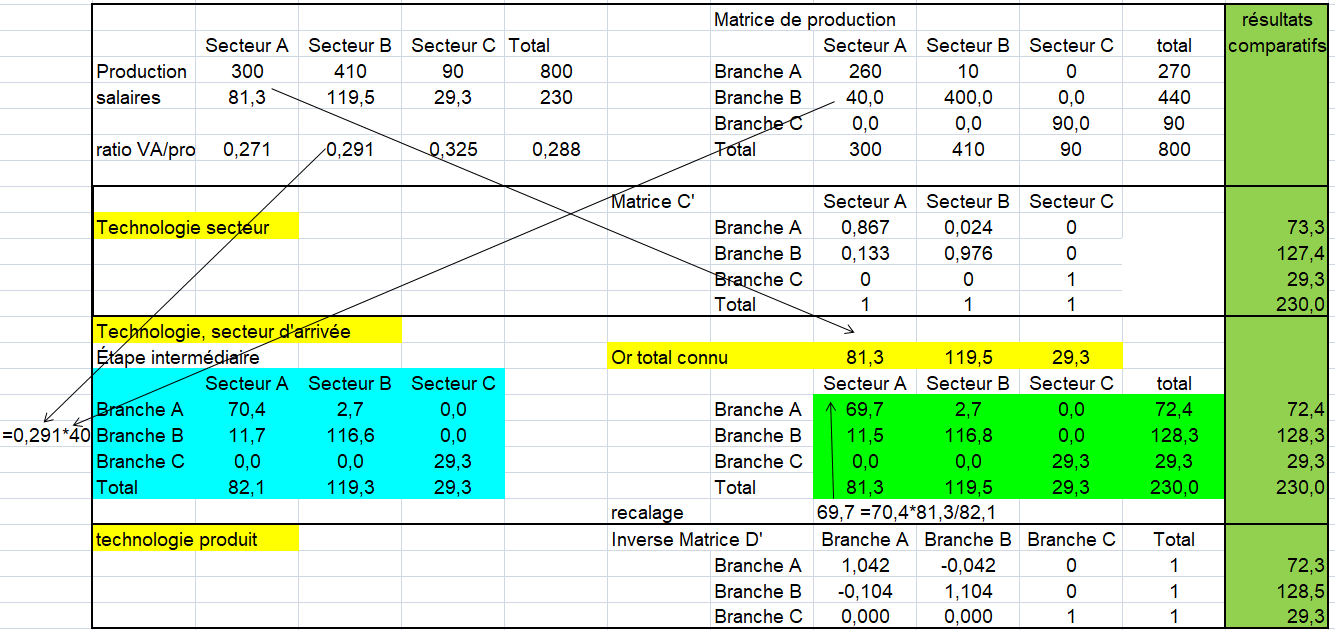
La France a mis au point une technologie intermédiaire, dite « technologie secteur d’arrivée » (TSA).

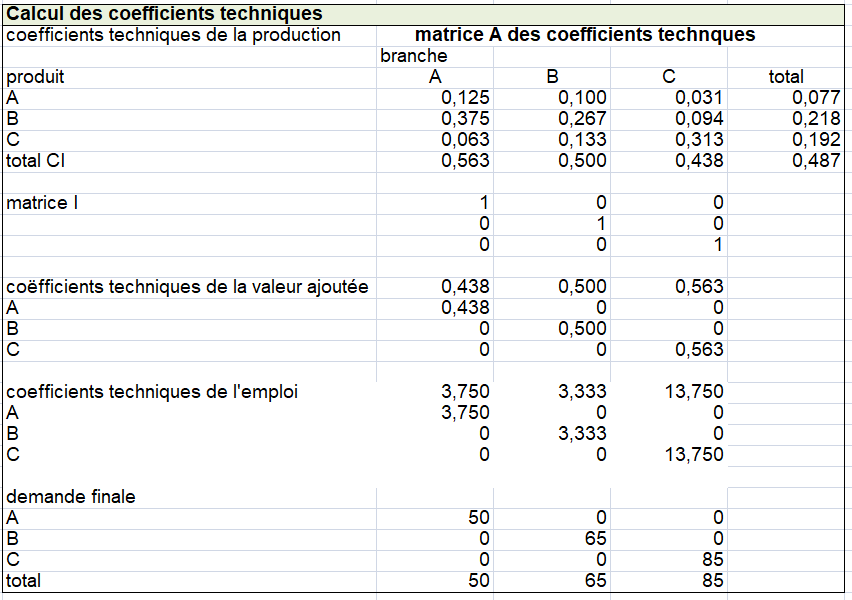
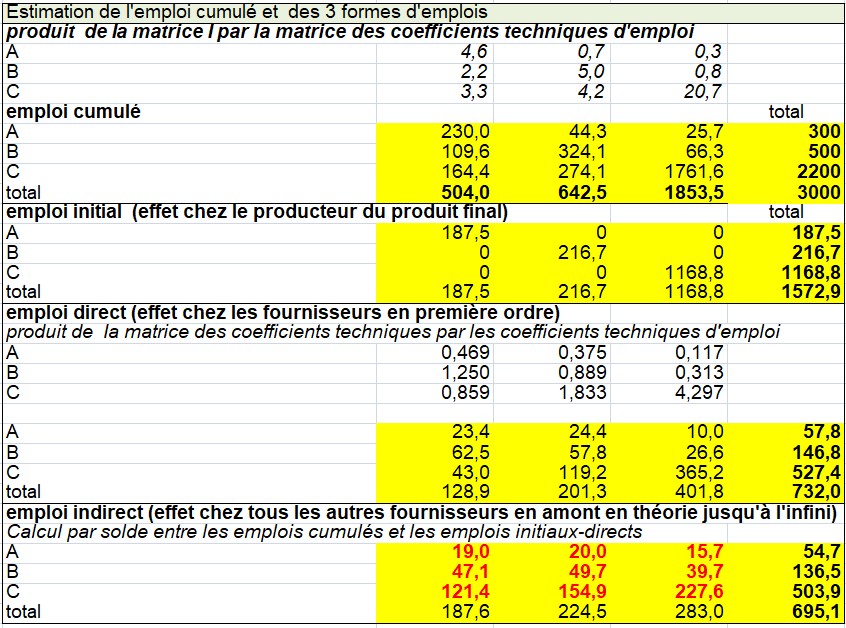
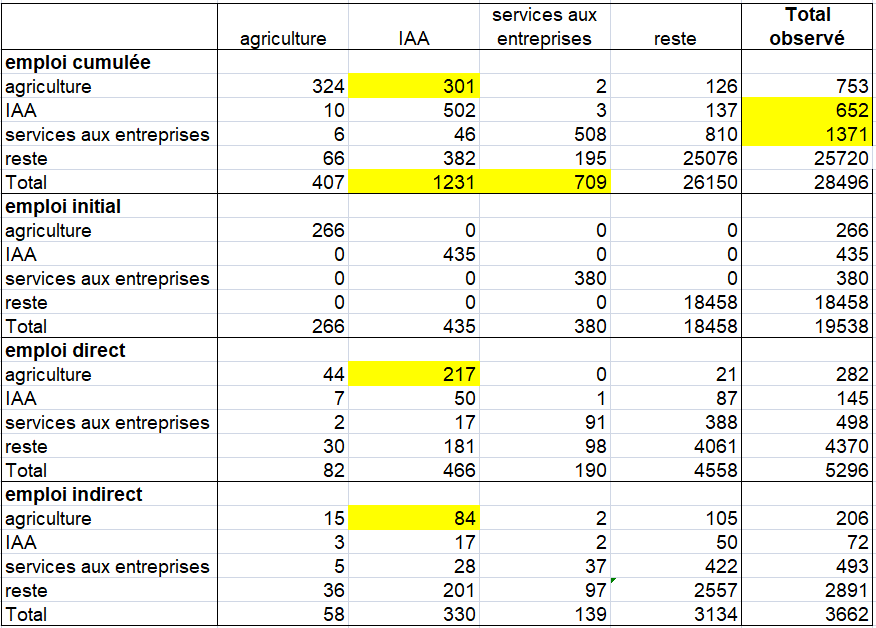
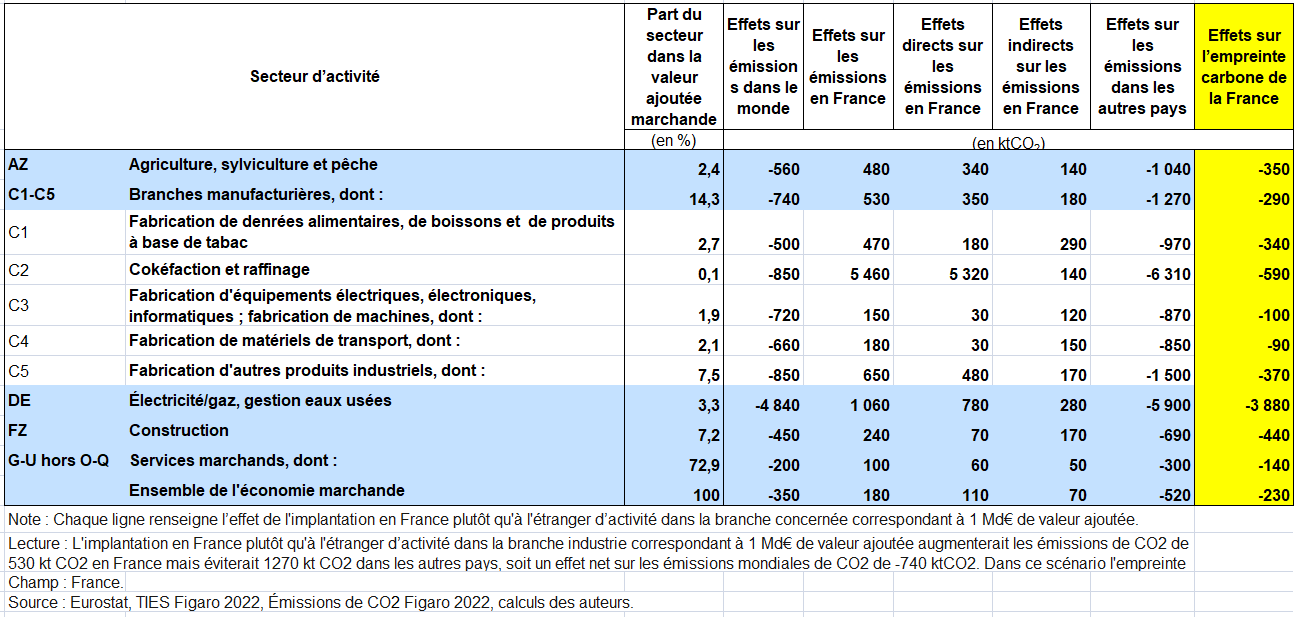
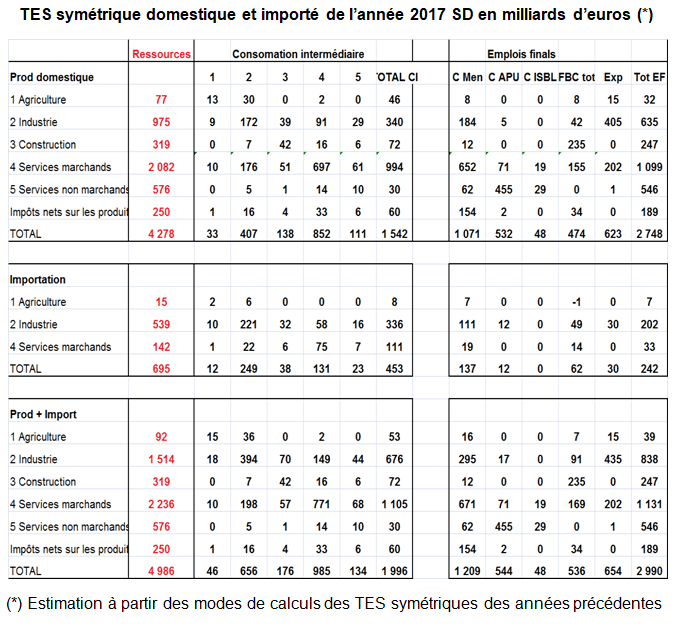
On propose un premier exemple fictif simple pour montrer les implications de ces différences. Quelles sont elles entre les TES symétriques par « industry » (branche d’établissement) et par produit?
La plupart des pays élaborent des TES par produits selon les principes de W. Leontief. Celui-ci a défini un tableau INPUT-OUTPUT par produit dans son livre « la structure de l’économie américaine (1939) ». Combien d’acier faut il pour produire une voiture? Dans ce TES par produit, l’hypothèse de technologie « produit » est plus correcte économiquement que l’hypothèse de la technologie par branche d’établissements (ou secteur d’activités).
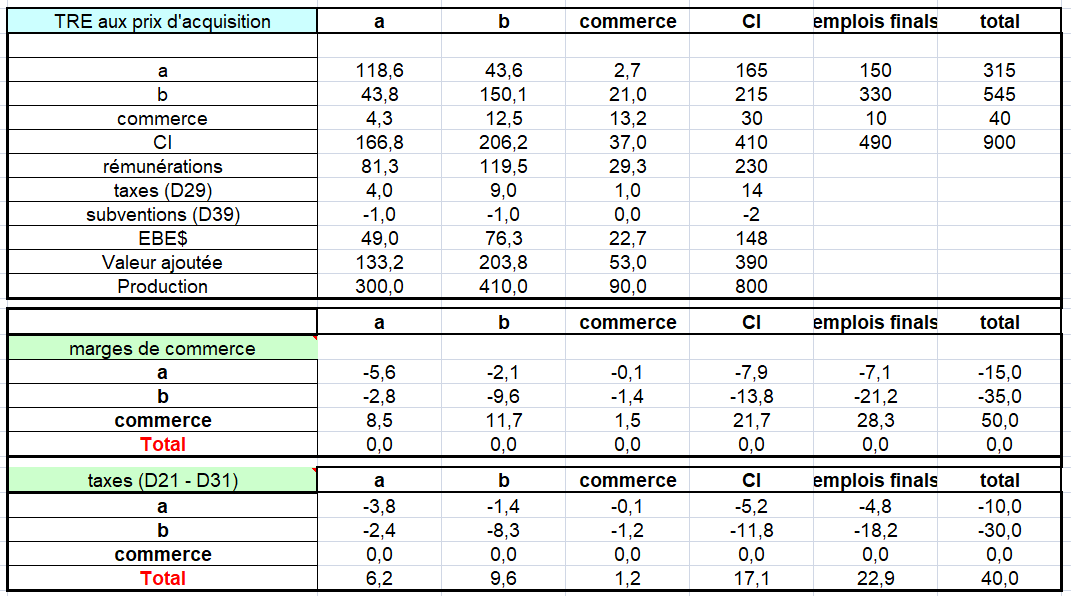
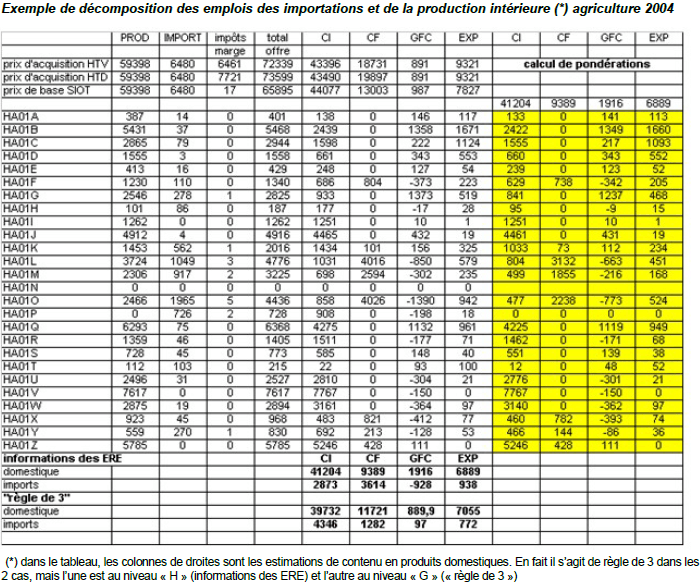
Mais les ERE par produits sont plus fragiles car ils reposent sur une ventilation des ventes de branche d’établissement (secteur d’activité) par produits. Or, il y a des imprécisions sur cette ventilation comme dans le cas français malgré les enquêtes auprès des entreprises. Un autre argument est d’éviter les données négatives (-16 dans l’exemple suivant pour la CI du produit agriculture par la branche agriculture). Ceci est très difficile à gérer dans les TES symétriques par produits (voir ci dessous).
C’est pourquoi quelques pays (Danemark, Pays-Bas, Norvège,..) préfèrent établir des TES symétriques par branche d’établissement. Leur argument est d’être au plus près des sources les plus connues (production par branche d’établissement ou par secteur d’activité connue par les enquêtes et les sources fiscales).







 –
–